<<主页
矩阵条件数
本模块演示了一个给定矩阵A的条件数(condition number)的几何解释,
矩阵条件数反映了这个矩阵作用于任意非零向量时可能产生的最大拉伸与最大压缩的比值, 它的严格定义是 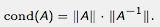 这个矩阵将2-范数度量下的单位圆变换为一个椭圆, 椭圆的长短
轴是这个矩阵作用于单位向量后产生最大拉伸或压缩得到的"像"(image). 因此, 矩阵的条件数就是这个椭圆长短轴长度的比值. 一个病态的矩阵会将单位圆变换成一个细长的"雪茄"或"针"的形状, 而经良态矩阵转换的单位圆, 它的像仍然很接近圆的形状. 通过矩阵的条件数可以估计线性方程组求解的误差限.
这个矩阵将2-范数度量下的单位圆变换为一个椭圆, 椭圆的长短
轴是这个矩阵作用于单位向量后产生最大拉伸或压缩得到的"像"(image). 因此, 矩阵的条件数就是这个椭圆长短轴长度的比值. 一个病态的矩阵会将单位圆变换成一个细长的"雪茄"或"针"的形状, 而经良态矩阵转换的单位圆, 它的像仍然很接近圆的形状. 通过矩阵的条件数可以估计线性方程组求解的误差限.
用户可以在左下方输入一个二阶矩阵的元素, 也可以使用程序预设的矩阵、或者随机生成一个矩阵(点击"Random"按钮). 对应于矩阵数据, 左侧绘图区显示一个单位圆, 而右侧则是经过这个矩阵变换得到的相应的 椭圆, 而绘图区下方显示出矩阵条件数的值. 右侧图形中的两个彩色箭头分别代表椭圆的长短轴, 它们的原像(preimage)则用同样的颜色显示在左侧图形中. 注意, 两个图形的缩放比例始终是一样的, 但为了使右侧绘图区的大小适应椭圆的尺寸, 对每个矩阵程序都要重新选择一次绘图的缩放比例.
操作与思考: 输入怎样的矩阵使条件数为1? 输入怎样的矩阵可使条件数尽可能大?
参考内容:课本3.1.3小节的有关内容.
