2. 评测算法详细介绍

2.1. BA算法 1

算法介绍

BA的全称是 Boundary Attack。该算法使用目标类中的一个样本初始化为非目标攻击，并用一个混合了均匀噪声的样本初始化为目标攻击。算法的每次迭代有三个部分。首先，通过二进制搜索将上次迭代的迭代结果推向边界。

接着，通过如下方程估计梯度方向。

\[\widetilde{\triangledown S} (x^t, \delta):=\frac{1}{B} \sum_{b=1}^{B} \phi_x(x^t+\delta_{u_b})u_b\]

最后通过几何级数选择合适的步长，直到扰动成功。并通过二元搜索将扰动样本推回边界。

参数说明

参数名称	参数说明
epsilon	扰动的步长系数
delta	重新缩放的扰动的尺寸
lower_bound	归一化数据上边界
upper_bound	归一化数据下边界
max_iter	扰动样本更新的最大内层迭代次数
binary_search_steps	搜索ε的迭代次数
batch_size	单次批处理大小
step_adapt	用来更新delta的更新系数
sample_size	过程中生成的潜在扰动样本的采样数目
init_size	初始化的随机样本数目

2.2. BIM算法 2

算法介绍

BIM全称为Basic Iterative Method。FGSM 这种one-step 方法通过一大步运算增大分类器的损失函数而进行图像扰动，因而可以直接将其扩展为通过多个小步增大损失函数的变体，从而我们得到 Basic Iterative Methods（BIM）。BIM是FGSM的拓展，进行了多次小步的迭代，并且在每一步之后都修剪得到的结果的像素值，来确保得到的结果在原始图像的 ϵ 邻域内，BIM迭代生成对抗样本的公式如下：

\[X_0^{adv}=X,\; \; X_{N+1}^{adv}=Clip_{X,\epsilon}\{ X_n^{adv} + \alpha sign(\triangledown _X J(X_N^{adv}, y_{true})) \}\]

参数说明

参数名称	参数说明
eps	原始样本的灰度偏移比例
eps_iter	梯度步长的改变比例
num_steps	多次迭代的次数

2.3. BLB算法 3

算法介绍

BLB的全称是 Box-constrained L-BFGS attack。该攻击方法通过对图像添加小量的人类察觉不到的扰动误导神经网络做出误分类：

\[min_{\rho}|| \rho ||_2 \; s.t. C(I_c + \rho) = l;\; I_c + \rho \in [0,1]^m\]

其中Ic∈R^{m表示一张干净的图片，ρ∈R}m是一个小的扰动，I是图像的label，C(…)是深度神经网络分类器。l和原本图像的label不一样。

但由于问题的复杂度太高，转而求解简化后的问题，即寻找最小的损失函数添加项，使得神经网络做出误分类，这就将问题转化成了凸优化过程。

\[min_{\rho} \; c|\rho| + L(I_c + \rho, l)\; \; s.t. I_c + \rho \in [0,1]^m\]

L(.,.)计算分类器的loss。通过凸优化的手段得到最终的噪音。

参数说明

参数名称	参数说明
init_const	二分搜索的参数的初始值，用于初始扰动图像的数据产生
binary_search_steps	二分搜索的一次循环步长
max_iter	使用LBFGS，torch的优化器优化扰动值的最大迭代次数

2.4. CW2算法 4

算法介绍

CW2算法的全称是 Carlini & Wagner Attack。Carlini 和Wagner 为了攻击防御性蒸馏(Defensive distillation)网络提出了三种对抗攻击方法，通过限制 l0,l1,l∞范数使得扰动无法被察觉。实验证明蒸馏网络完全无法防御这三种攻击。该算法生成的对抗扰动可以从unsecured网络迁移到secured网络上，从而实现黑箱攻击。实验表明，C&W攻击方法能有效攻击现有的大多数防御方法。

目标函数表示为：

\[min_{\delta} D(x,x+\delta)+c \cdot f(x+\delta)\, subject \; to \; x + \delta \in [0,1]\]

式中，δ 是对抗扰动；D(∙,∙)表示L0、L2或L∞距离度量；f(x +δ)是自定义的对抗损失，当且仅当DNN的预测为攻击目标时才满足f(x +δ)≤0。为了确保x + δ产生能有效的

图像（即x +δ ∈ [0, 1]），引入了一个新变量来代替δ：

\[\delta = \frac{1}{2}(tanh(K) + 1) - x\]

这样，x + δ =1/2(tanh(k) + 1)在优化过程中始终位于[0, 1]中。除了在MNIST、CIFAR10和ImageNet的正常训练DNN模型上获得100%的攻击成功率外，C&W攻击还可以破坏防御性蒸馏模型，而这些模型可以使L-BFGS和Deepfool无法找到对抗性样本。

参数说明

参数名称	参数说明
dataset	使用的数据集的名称
class_type_num	分类网络的类别
kappa	标签的序号的整体偏移量
learning_rate	迭代过程中优化器的学习率
init_const	初始的迭代求解参数的值
lower_bound	产生中间扰动样本的值的下边界
upper_bound	产生中间扰动样本的值的上边界
max_iter	为了生成合适的扰动样本时候的迭代次数
binary_search_steps	为了求解合适的参数的搜索迭代次数

2.5. Deepfool算法 5

算法介绍

对于多分类问题，通常采取的方案为一对多。在这里，针对多个输出类别，通过下式进行分类选择：

\[\hat{k}(x)=\underset{k}{arg\, max}f_k(x)\]

对于线性多分类器，我们有：

\[f(x)=W^Tx+b\]

最小扰动可以由下式计算：

\[\begin{split}\\ \underset{r}{arg\, min}\left |\left |r \right | \right |_2 \\ s.t. \; \exists k: w_k^T(x_0 + r) + b_k \geq w_{\hat{k}(x_0)}^T(x_0+r)+b_{\hat{k}(x_0)}\end{split}\]

为了解这个问题，我们先来看一个四分类问题的例子：

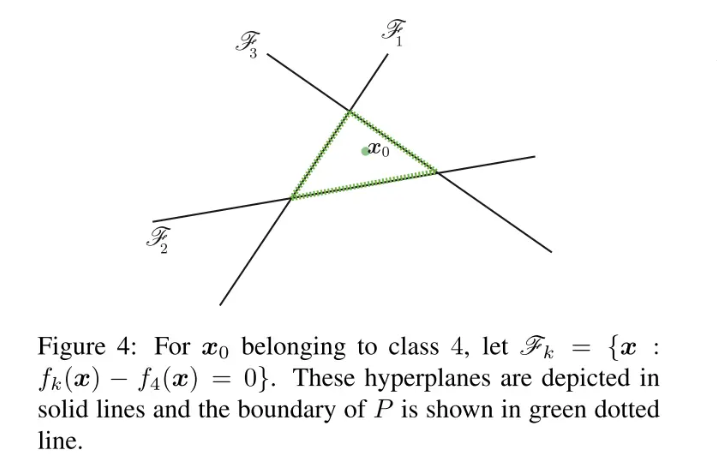
注意，这里只有三条线，分别对应前三类的参数超平面与第四类相减得到的参数超平面。同样利用点到直线的距离公式，若求得到这三条线的最短距离便可得到使样本分类发生变化的最小扰动长度。最短距离可以用下式计算：

\[\hat{l}(x_0)=\underset{k\neq \hat{k}(x_0)}{arg \, min} \frac{\left| f_k(x_0) - f_{\hat{k}(x_0)}(x_0) \right |}{\left | \left | w_k - w_{\hat{k}(x_0)} \right | \right |_2}\]

因此最小扰动向量为：

\[r_*(x_0)=\frac{\left| f_{\hat{l}(x_0)}(x_0) - f_{\hat{k}(x_0)}(x_0) \right |}{\left | \left | w_{\hat{l}(x_0)} - w_{\hat{k}(x_0)} \right | \right |_2^2}(w_{\hat{l}(x_0)} - w_{\hat{k}(x_0)})\]

对于一般的多分类问题，同样利用近似线性的方法迭代得到，算法如下：

注意，这个算法并不能保证收敛到最小扰动解。算法中2范数可以扩展到p范数。

参数说明

参数名称	参数说明
overshoot	防止算法收敛到分类面上
max_iter	为了生成合适的扰动样本时候的迭代次数

2.6. FGSM算法 6

算法介绍

FGSM的全称是Fast Gradient Sign Method(快速梯度下降法），在白盒环境下，通过求出模型对输入的导数，然后用符号函数得到其具体的梯度方向，接着乘以一个步长，得到的“扰动”加在原来的输入 上就得到了在FGSM攻击下的样本。

FGSM的攻击表达如下：

\[x^{'}=x+\varepsilon \cdot sign(\triangledown_x J(x, y))\]

攻击成功就是模型分类错误，就模型而言，就是加了扰动的样本使得模型的loss增大。而所有基于梯度的攻击方法都是基于让loss增大这一点来做的。可以仔细回忆一下，在神经网络的反向传播当中，我们在训练过程时就是沿着梯度方向来更新更新w，b的值。这样做可以使得网络往loss减小的方向收敛。

\[\begin{split}\\ W_{ij}^{(l)}=W_{ij}^{(l)}-\alpha \frac{\partial}{\partial W_{ij}^{(l)}}J(W,b) \\ b_{i}^{(l)}=b_{i}^{(l)}-\alpha \frac{\partial}{\partial b_{i}^{(l)}}J(W,b)\end{split}\]

那么现在我们既然是要使得loss增大，而模型的网络系数又固定不变，唯一可以改变的就是输入，因此我们就利用loss对输入求导从而“更新”这个输入。

参数说明

参数名称	参数说明
epsilon	沿着梯度的步长系数

2.7. JSM算法 7

算法介绍

JSM算法的全称是Jacobian-based Saliency Map Attack

目标是只修改图像中的几个像素，而不是扰乱整个图像来欺骗分类器,该算法一次修改一个干净图像的像素，并监测变化对结果分类的影响。通过使用网络层的输出的梯度来计算一个显著性图来执行监控。

JSMA算法主要包括三个过程：计算前向导数，计算对抗性显著图，添加扰动，以下给出具体解释。

所谓前向导数，其实是计算神经网络最后一层的每一个输出对输入的每个特征的偏导。以MNIST分类任务为例，输入的图片的特征数（即像素点）为784，神经网络的最后一层一般为10个输出（分别对应0-9分类权重），那对于每一个输出我们都要分别计算对784个输入特征的偏导，所以计算结束得到的前向导数的矩阵为（10，784）。前向导数标识了每个输入特征对于每个输出分类的影响程度，其计算过程也是采用链式法则。这里需要说明一下，前面讨论过的FGSM和DeepFool不同在计算梯度时，是通过对损失函数求导得到的，而JSMA中前向导数是通过对神经网络最后一层输出求导得到的。前向导数∇F(X)具体计算过程如下所示，j表示对应的输出分类，i表示对应的输入特征。

\[\begin{split}\\ \triangledown F(X)=\frac{\partial F(X)}{\partial X}=\left [ \frac{\partial F_j(X)}{\partial x_i} \right ]_{i \in 1...M,j \in 1...N} \\ \frac{\partial F_j(X)}{\partial x_i}=\left( W_{n+1,j} \cdot \frac{\partial H_n}{\partial x_i} \right ) \times \frac{\partial f_{n+1,j}}{\partial x_i}\left( W_{n+1,j} \cdot H_n + b_{n + 1, j} \right )\end{split}\]

通过得到的前向导数，我们可以计算其对抗性显著图，即对分类器特定输出影响程度最大的输入。首先，根据扰动方式的不同（正向扰动和反向扰动），作者提出了两种计算对抗性显著图的方式，即：

\[\begin{split}S(X,t)[i]= \left\{\begin{matrix} 0 & if \: \frac{\partial F_t(X)}{\partial X_i} < 0 \: or \: \sum_{j \neq t} \frac{\partial F_j(X)}{\partial X_i} > 0 \\ \left( \frac {\partial F_t(X)}{\partial X_i} \left | \sum_{j \neq t} \frac{\partial F_j(X)}{\partial X_i} \right | \right ) & otherwise \end{matrix}\right.\end{split}\]

但是在文章中第四部分的应用中作者发现，找到单个满足要求的特征很困难，所以作者提出了另一种解决方案，通过对抗性显著图寻找对分类器特定输出影响程度最大的输入特征对，即每次计算得到两个特征。

\[argmax_{p1,p2}\left( \sum_{i=p1,p2} \frac{\partial F_t(X)}{\partial X_i} \right) \times \left| \sum_{i=p1,p2} \sum_{j \neq t} \frac{\partial F_j(X)}{\partial X_i} \right |\]

算法具体过程：

参数说明

参数名称	参数说明
theta	样本一维度化之 后（拉平）对图像的灰度的增减。小于0是降低，大于0是增加。
gama	决定迭代次数的和图像尺度大小相关的一个比例系数

2.8. PGD算法 8

算法介绍

PGD全称是Projected Gradient descent。目的是为解决FGSM和FGM中的线性假设问题，使用PGD方法来求解内部的最大值问题。 PGD是一种迭代攻击，相比于普通的FGSM和FGM 仅做一次迭代，PGD是做多次迭代，每次走一小步，每次迭代都会将扰动投射到规定范围内。

\[g_t=\triangledown X_t(L(f_\theta (X_t), y))\]

gt 表示t时刻的损失关于t时刻输入的梯度。

\[X_{t+1} = \prod _{X+S}(X_t+\varepsilon (\frac{g_t}{|| g_t ||}))\]

t+1时刻输入根据t时刻的输入及t时刻的梯度求出。∏_(X+S)的意思是，如果扰动超过一定的范围，就要映射回规定的范围S内。

由于每次只走很小的一步，所以局部线性假设基本成立。经过多步之后就可以达到最优解，也就是达到最强的攻击效果。同时使用PGD算法得到的攻击样本，是一阶对抗样本中最强的。这里所说的一阶对抗样本是指依据一阶梯度的对抗样本。如果模型对PGD产生的样本鲁棒，那基本上就对所有的一阶对抗样本都鲁棒。实验也证明，利用PGD算法进行对抗训练的模型确实具有很好的鲁棒性。

PGD虽然简单，也很有效，但是存在一个问题是计算效率不高。不采用提对抗训练的方法m次迭代只会有m次梯度的计算，但是对于PGD而言，每做一次梯度下降（获取模型参数的梯度，训练模型），都要对应有K步的梯度提升（获取输出的梯度，寻找扰动）。所以相比不采用对抗训练的方法，PGD需要做m(K+1)次梯度计算。

参数说明

参数名称	参数说明
eps	原始样本的灰度偏移比例
eps_iter	梯度步长的改变比例
num_steps	迭代次数

2.9. SPSA算法 9

算法介绍

SPSA算法全称是Multivariate stochastic approximation using a simultaneous perturbation gradient approximation

SPSA算法非常适合于高维优化问题，即使在不确定目标的情况下，我们也可使用SPSA公式来产生对抗性攻击。在SPSA算法中，首先从Rademacher分布（即Bernoulli±1）中抽取一批n个样本，即

\[v1,...,vn ∈\{1, -1\}^D\]

然后用随机方向上的有限差分估计逼近梯度。具体来说，对于第i个样本，估计的梯度gi计算如下：

\[g_i=\frac{f(x_t+\delta v_i) - f(x - \delta v_i)}{2\delta v_i}\]

式中，δ是扰动大小，xt是第t次迭代时的扰动图像，f是要评估的模型。最后，SPSA对估计的梯度进行聚合，并在输入文本上执行投影梯度下降。整个过程按预先确定的迭代次数进行迭代。

完整的伪代码如下：

参数说明

参数名称	参数说明
alpha	沿着梯度扰动的步长系数
gamma	扰动的系数
c_par	迭代的基准噪声系数
a_par	用来调整alpha系数的更新系数
sizeN	扰动样本更新的最大内层迭代次数
min_vals_iter	最小的loss值下界
print_every	迭代过程中多少次迭代后打印一次
max_iter	扰动样本更新的最大外层迭代次数

2.10. UAP算法 10

算法介绍

UAP算法的全称是Universal Adversarial Perturbation attack。

UAP算法提出了一种不易察觉的万能perturbation，它能使目前最好的分类器，在完成图片分类任务时出错。通过这个算法得到的perturbation，在各种神经网络情况下都能取得很好的效果。这揭示了目前分类器分类“判定边界”在高维度上的几何关系。

万能perturbation的构造算法：

算法得到的perturbation需要满足两个条件：

\[\begin{split}\\ ||v||_p \leq \xi \\ \underset{x \sim u}{\mathbb{P}}(\hat{k}(x+v) \neq \hat{k}(x)) \geq 1 - \delta\end{split}\]

即第一是扰动的规模要比较小，第二是原来的数据叠加了扰动之后，分类器的输出错误率要大于一个阈值。整体的算法如下：

其算法思想是对于图片数据中的每一个点，依次计算能使得最终分类器的输出错误的最小扰动，一直循环知道将整体分类错误的概率大于 1 − δ，其中 δ 为人为定义的分类器准确度。而算法的关键不是为了找到一个能使大多数样本分类错误的最小perturbation，而是用足够小的范数找到这样的一个扰动。

参数说明

参数名称	参数说明
dataset	使用的数据集类别

2.11. MIM算法 11

算法介绍

MIM算法全称是Momentum Iterative Fast Gradient Sign Method(UMI-FGSM)。

在迭代攻击方法中加入动量项（momentum term），提高对抗样本的转移性：

\[\begin{split}\\ g_{t+1}=\mu \cdot g_t + \frac{\triangledown_x J(x_t^{adv}, y)}{|| \triangledown_x J(x_t^{adv}, y) ||_1} \\ x_{t+1}^{adv}=x_{t}^{adv}+\alpha \cdot sign(g_{t+1})\end{split}\]

其中gt包含了直到t次迭代的梯度信息。

参数说明

参数名称	参数说明
epsilon	扰动的步长系数
eps_iter	调节扰动的步长的比例系数
num_step	扰动样本更新的迭代次数
decay_factor	调节动量项的步长

2.12. ZOO算法 12

算法介绍

ZOO算法全称为Zeroth Order Optimization Based Black-box。

ZOO攻击不可知，仅依赖于预测分数（例如类别机率或对数），使用数值估算梯度的预测。ZOO算法利用正负扰动带来的概率差估算一阶导（梯度）和二阶导，再利用ADAM或者牛顿法等方法更新x。本质为通过估算梯度将黑盒转换为白盒过程。

ZOO算法的损失函数和CW相似：

\[minimize_x ||x-x_0||_2^2+c\cdot f(x,t) \; \; subject \; to \; x \in [0,1]^p\]

损失函数如上，左边保证对抗样本与真实input的相似，右边保证对抗样本能导致目标模型出错，具体如下：

目标攻击下：

\[f(x,t)=max\{ \underset{i \neq t}{max} log[F(x)]_i - log[F(x)]_t, -K \}\]

非目标下

\[f(x)=max\{log[F(x)]_{t_0} - \underset{i \neq t}{max} log[F(x)]_i , -K \}\]

随机选取一个坐标

估计梯度，h非常小，ei是一个只有i-th元素等于1的偏置向量。第二个只在牛顿法中才会使用。

\[\begin{split}\\ \hat{g}_i :=\frac{\partial f(x)}{\partial x_i} \approx \frac{f(x+he_i) - f(x - he_i)}{2h} \\ \hat{h}_i := \frac{\partial ^2 f(x)}{\partial x_{ii}^2} \approx \frac{f(x+he_i) - 2f(x) + f(x - he_i)}{h^2}\end{split}\]

参数说明

参数名称	参数说明
solver	解算方法，Adam/Newton/Newton Adam
resize_init_size	输入图像调整后尺寸
img_h	图像高度
img_w	图像宽度
num_channels	图像通道数
use_resize	是否需要调整图像尺寸
class_type_number	分类类别数目
use_tanh	是否转化到tanh函数空间
confidence	班主判断攻击类别和预测类别是否相同或有固定偏差
batch_size	批处理大小
init_const	Loss1初始化的调节系数（放大率）
max_iter	最大迭代次数
binary_search_steps	用于搜索初始CONST的迭代次数
beta1	用于产生中间图像数据的调节系数1
beta2	用于产生中间图像数据的调节系数2
lr	用于更新原有数据和梯度，以及二阶导数关系的调节系数
reset_adam_after_found	是否在找到参数后重置adam
early_stop_iters	提早结束的迭代次数
ABORT_EARLY	没有提升是否提前中断
lower_bound	转化到tan函数空间的数据归一化下边界
upper_bound	转化到tan函数空间的数据归一化上边界
print_every	迭代过程的打印间隔
use_log	是否保存过程中的Loss值
save_modifier	是否保存过程中的攻击样本和原样本差值（修改值）
load_modifier	是否载入过程中的攻击样本和原样本差值（修改值）
use_importance	是否使用概率方法选择生成数据挑选次序

2.13. Auto-PGD算法 13

算法介绍

Auto-PGD是一种基于PGD改进， 在其基础上加入动量方法、重启方法及步长衰减， 从而实现自适应地调整迭代步长，避免超参的设置。 伪代码如下：

参数说明

参数名称	参数说明
eps	原始样本的灰度偏移比例
n_iter	最大迭代的次数

2.14. SimBA算法 14

算法介绍

SimBA全称为Simple Black-box Adversarial Attack。 SimBA是一种黑盒攻击算法，运行时在输入维度上不重复地选取一个加上ε， 观察标签类别的置信度是否下降，若下降则接受这步迭代， 否则反向走一步。伪代码如下：

参数说明

参数名称	参数说明
epsilon	迭代步长
max_iters	最大迭代的次数

2.15. Sign Hunter算法 15

算法介绍

Sign Hunter算法是一种黑盒攻击算法，旨在提高查询效率。 与直接估算模型梯度相比，估算模型梯度的符号更容易实现，效果接近白盒攻击算法FGSM。 攻击扰动在H={ε, -ε}ⁿ上取，问题转化为最大化方向导数

\[max_{q\in H}D_q L(x,y)\]

初始时取全正和全负各算一次损失函数，较大者说明估计正确的符号较多，接收这一步迭代， 第二轮翻转一半的符号，之后每当所有维度都检查过后，翻转区间c_len减半，进行更细粒度的检查

参数说明

参数名称	参数说明
epsilon	原始样本的灰度偏移比例
max_queries	最大查询的次数

2.16. Square Attack算法 16

算法介绍

Square Attack算法是一种不依赖于梯度估计的黑盒攻击算法。 Square Attack基于随机搜索，但不是完全随机的噪声，而是选择方形的区域。 选定区域后各个颜色通道独立在范围内选择增量。选择的区域大小可根据不同策略调整，此处实现的是迭代特定次数后减半。

参数说明

参数名称	参数说明
epsilon	原始样本的灰度偏移比例
n_iters	最大迭代次数
p_init	初始选择区域大小

2.17. N-Attack算法 17

*仅适用于cifar模型 N-Attack是一种黑盒攻击算法，使用输入附近的正态分布对梯度进行估计

\[\nabla f(x_t)\approx\nabla_{x_t}\mathbb{E}_{N(z|x_t,\sigma^2)}f(z)=\mathbb{E}_{N(z|x_t,\sigma^2)}f(z)\nabla_{x_t}log N(z|x_t,\sigma^2)\]

再用估计的梯度进行梯度下降。

参数名称	参数说明
n_samples	每轮采样数量
sigma	随机采样标准差
lr	每步迭代步长
epsilon	原始样本的灰度偏移比例
n_iter	最大迭代次数

2.18. P-RGF算法 18

P-RGF全称prior-guided random gradient-free， 是一种利用迁移梯度的score-based黑盒算法。

在RGF方法中，可抽取多个单位偏移估计当前位置的梯度，如下式

\[\hat{g}=\frac{1}{q}\sum_{i=1}^q\hat{g_i},\hat{g_i}= \frac{f(x+\sigma u_i,y)-f(x,y)}{\sigma}\cdot u_i\]

其中u是随机单位向量。这个估计方法的损失函数为

\[\lim_{\sigma\to0}L(\hat{g})=||\nabla f(x)||^2_2-\frac{(\nabla f(x)^TC\nabla f(x))^2}{(1-\frac{1}{q})\nabla f(x)^TC^2\nabla f(x)+\frac{1}{q}\nabla f(x)^TC\nabla f(x)}\]

其中C是选取的随机向量的协方差矩阵。P-RGF方法是令迁移梯度作为C的一个特征向量，那么C可以分解为

\[C=\lambda vv^T+\frac{1-\lambda}{D-1}(I-vv^T)\]

此时对应选择的单位偏移u为

\[u_i=\sqrt{\lambda}v+\sqrt{1-\lambda}\widehat{(I-vv^T)\xi_i}\]

参数λ的选择可以是固定值，也可以根据迁移梯度与黑盒梯度的余弦相似度的估计值调整

参数说明

参数名称	参数说明
epsilon	原始样本的灰度偏移比例
max_queries	最大查询次数
n_sample	每次抽取随机向量个数

2.19. Sign-OPT算法 19

算法介绍

Sign-OPT算法是一种decision-based黑盒算法。 首先对一个方向θ进行二分查找，找到该方向上的分类边界，定义损失函数g：

\[g(θ) = arg min_{λ>0}(f(x_0+λ\hat{θ})\neq y_0)\]

这个函数的方向导数可以通过以下差分估算：

\[\hat\nabla g(\theta;u):=\frac{g(\theta+\epsilon u)-g(\theta)}{\epsilon}u\]

其中u是随机向量。如图，此操作相当于在分类边界上向随机方向前进一小步， 通过分类标签是否仍为y0判断方向导数的符号。

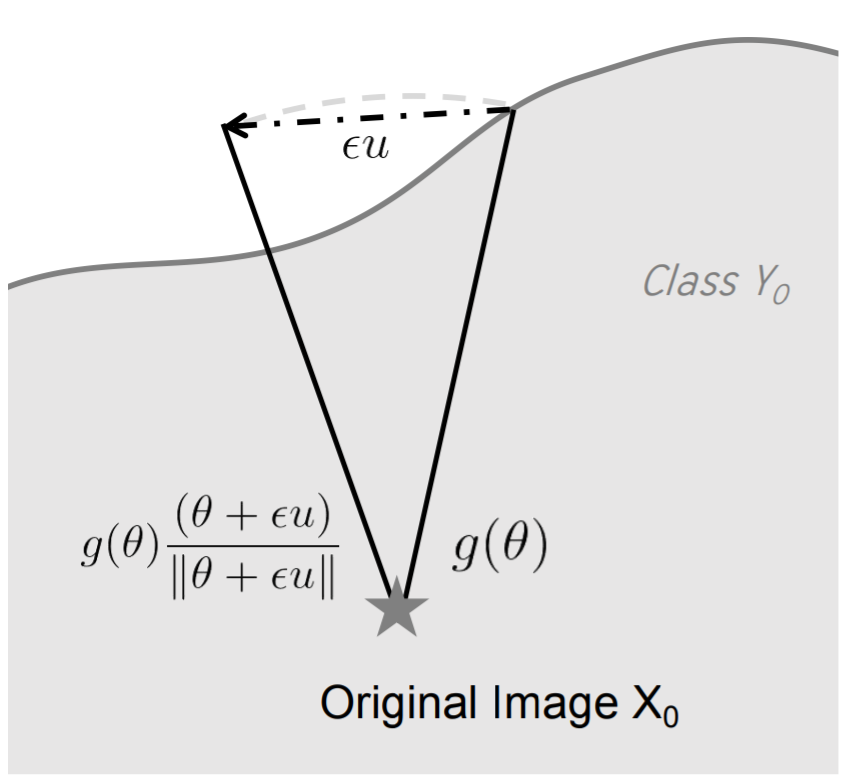
多次求取不同方向上的导数符号可用于估算梯度方向， 最终实现函数g在分类界面上的梯度下降。

参数说明

参数名称	参数说明
n_iter	梯度下降步数
query_limit	最大查询次数
n_sample	每轮采样点数

2.20. Evolutionary Attack算法 20

Evolutionary attack算法是一种黑盒攻击算法，主要用于面部识别模型的对抗样本生成， 通过向不同方向二分查找找到分类界面，并优化查找方向， 找到与目标比较接近的分类界面上的点作为对抗样本的输出。

参数名称	参数说明
num_queries	查询次数
sigma	随机采样标准差

2.21. DIM算法 21

算法介绍

DIM算法全称Diverse Input Method，是一种基于迁移的黑盒攻击算法。 在使用代理模型进行梯度计算时，对输入进行一些变换来避免对代理模型的过拟合。 在该算法中用到的变换是缩放和平移。

参数说明

参数名称	参数说明
epsilon	扰动的步长系数
eps_iter	调节扰动的步长的比例系数
num_step	扰动样本更新的迭代次数
decay_factor	调节动量项的步长
resize	图片缩放的最小尺寸
prob	选择变换后的输入的概率
model_name	代理模型名称
model_path	代理模型参数，默认从torchvision下载

2.22. TIM算法 22

算法介绍

TIM算法全称Translation-Invariant Attacks，是一种基于迁移的黑盒攻击算法。 在使用代理模型进行梯度计算时， 对输入进行一些平移来消除图像位置信息带来的干扰， 从而提高对抗样本的迁移性。

参数说明

参数名称	参数说明
epsilon	扰动的步长系数
eps_iter	调节扰动的步长的比例系数
num_step	扰动样本更新的迭代次数
decay_factor	调节动量项的步长
prob	选择变换后的输入的概率
model_name	代理模型名称
model_path	代理模型参数，默认从torchvision下载

2.23. NIM算法 23

算法介绍

NIM算法是一种基于迁移的黑盒攻击算法。 在使用代理模型进行梯度计算时使用Nesterov Accelerated Gradient， 这是一种变种的梯度下降法，可以提高收敛速度。

\[ \begin{align}\begin{aligned}x^{nes}_t=x^{adv}_t+\alpha\mu g_t\\g_{t+1}=\mu g_t+\frac{\nabla_xJ(x^{nes}_t,y)}{||\nabla_xJ(x^{nes}_t,y)||_1}\\x^{adv}_{t+1}=x^{adv}_t+\alpha sign(g_{t+1})\end{aligned}\end{align} \]

参数说明

参数名称	参数说明
epsilon	扰动的步长系数
eps_iter	调节扰动的步长的比例系数
num_step	扰动样本更新的迭代次数
decay_factor	调节动量项的步长
prob	选择变换后的输入的概率
model_name	代理模型名称
model_path	代理模型参数，默认从torchvision下载

2.24. 参考文献

1

Brendel, Wieland, Jonas Rauber, and Matthias Bethge. “Decision-Based Adversarial Attacks: Reliable Attacks Against Black-Box Machine Learning Models.” International Conference on Learning Representations. 2018.

2

Kurakin, Alexey, Ian J. Goodfellow, and Samy Bengio. “Adversarial examples in the physical world.” Artificial intelligence safety and security. Chapman and Hall/CRC, 2018. 99-112.

3

Szegedy, C., Zaremba, W., Sutskever, I., Bruna, J., Erhan, D., Goodfellow, I., & Fergus, R. (2013). Intriguing properties of neural networks. arXiv preprint arXiv:1312.6199.

4

Carlini, Nicholas, and David Wagner. “Towards evaluating the robustness of neural networks.” 2017 IEEE symposium on security and privacy (sp). IEEE, 2017.

5

Moosavi-Dezfooli, Seyed-Mohsen, Alhussein Fawzi, and Pascal Frossard. “Deepfool: a simple and accurate method to fool deep neural networks.” Proceedings of the IEEE conference on computer vision and pattern recognition. 2016.

6

Goodfellow, Ian J., Jonathon Shlens, and Christian Szegedy. “Explaining and harnessing adversarial examples.” arXiv preprint arXiv:1412.6572 (2014).

7

Papernot, Nicolas, et al. “The limitations of deep learning in adversarial settings.” 2016 IEEE European symposium on security and privacy (EuroS&P). IEEE, 2016.

8

Kurakin, Alexey, Ian Goodfellow, and Samy Bengio. “Adversarial machine learning at scale.” arXiv preprint arXiv:1611.01236 (2016).

9

Uesato, Jonathan, et al. “Adversarial risk and the dangers of evaluating against weak attacks.” International Conference on Machine Learning. PMLR, 2018.

10

Moosavi-Dezfooli, Seyed-Mohsen, Alhussein Fawzi, Pascal Frossard, and Patrick McDaniel. “Universal adversarial perturbations.” Proceedings of the IEEE conference on computer vision and pattern recognition. 2017.

11

Dong, Yinpeng, et al. “Boosting adversarial attacks with momentum.” Proceedings of the IEEE conference on computer vision and pattern recognition. 2018.

12

Chen, Pin-Yu, et al. “Zoo: Zeroth order optimization based black-box attacks to deep neural networks without training substitute models.” Proceedings of the 10th ACM workshop on artificial intelligence and security. 2017.

13

Croce, Francesco, and Matthias Hein. “Reliable evaluation of adversarial robustness with an ensemble of diverse parameter-free attacks.” International conference on machine learning. PMLR, 2020.

14

Guo, Chuan, et al. “Simple black-box adversarial attacks.” International Conference on Machine Learning. PMLR, 2019.

15

Al-Dujaili, Abdullah, and Una-May O’Reilly. “Sign bits are all you need for black-box attacks.” International Conference on Learning Representations. 2019.

16

Andriushchenko, Maksym, et al. “Square attack: a query-efficient black-box adversarial attack via random search.” European Conference on Computer Vision. Springer, Cham, 2020.

17

Li, Yandong, et al. “Nattack: Learning the distributions of adversarial examples for an improved black-box attack on deep neural networks.” International Conference on Machine Learning. PMLR, 2019.

18

Cheng, Shuyu, et al. “Improving Black-box Adversarial Attacks with a Transfer-based Prior.” Advances in Neural Information Processing Systems 32 (2019): 10934-10944.

19

Cheng, Minhao, et al. “Sign-OPT: A Query-Efficient Hard-label Adversarial Attack.” International Conference on Learning Representations. 2019.

20

Dong, Yinpeng, et al. “Efficient decision-based black-box adversarial attacks on face recognition.” Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2019.

21

Xie, Cihang, et al. “Improving transferability of adversarial examples with input diversity.” Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2019.

22

Dong, Yinpeng, et al. “Evading defenses to transferable adversarial examples by translation-invariant attacks.” Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2019.

23

Lin, Jiadong, et al. “Nesterov Accelerated Gradient and Scale Invariance for Adversarial Attacks.” International Conference on Learning Representations. 2019.